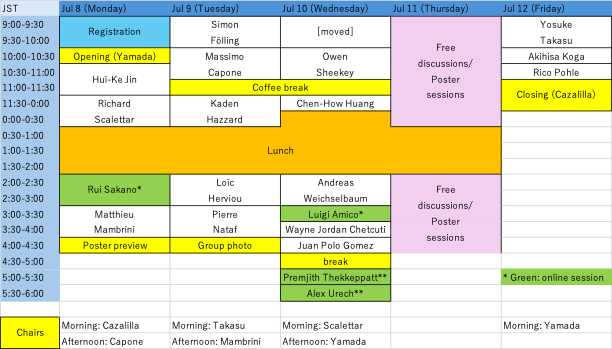
Program

Program (v3.0 release 20240707)

Here, JST = Japan Standard Time = UTC+9.

** Premjith Thekkeppatt and Alex Urech are from Florian Schreck's group.

Abstract booklet

• v2.0 release 20240524

In order to promote the SDGs, we only have a few copies of abstract booklets. If you need a paper booklet, please print this pdf out in advance by yourselves.

Online posters (PDF up to 1MB)

PDFs will be made public until the workshop ends.

If you have any questions to each poster, please ask them to the authors directly. We cannot answer anything on the contents of the online posters.

Yuki Amari

Skyrmion crystals with spin-nematic order in SU(3) chiral magnets

In this poster, we theoretically study skyrmion crystals that locally possess spin-nematic order (see figures below), where spin-nematic is a typical example of quantum liquid crystals. The skyrmion crystals appear as the ground state in SU(3) chiral magnets, which are SU(3) magnets endowed with a generalized Dzyaloshinskii-Moriya interaction. The system could be implemented using spin-1 spinor Bose-Einstein condensates with an artificial spin-orbit coupling in an optical lattice. We clarify the properties of the skyrmion crystals using several physical quantities like energy, topological charge and structure factors, and also map out the phase diagram.

Mateo Fontaine

Symmetry, topology, duality, chirality, and criticality in a spin-1/2 XXZ ladder with a four-spin interaction

We study the ground-state phase diagram of a spin-1/2 XXZ model with a chirality-chirality interaction (CCI) on a two-leg ladder. This model offers a minimal setup to study an interplay between spin and chirality degrees of freedom. The spin-chirality duality transformation allows us to relate the regimes of weak and strong CCIs. By applying the Abelian bosonization and the duality, we obtain a rich phase diagram that contains distinct gapped featureless and ordered phases.Two distinct symmetry protected topological (SPT) phases appear for easy-plane anisotropy. The two SPT phases can be viewed as twisted variants of the Haldane phase. We perform numerical simulations to confirm the predicted phase structure and critical properties. We further demonstrate that the two SPT phases and a trivial phase are distinguished by topological indices in the presence of certain symmetries. A similar phase structure is expected in a spin- 1/2 XXZ ladder with four-spin ring exchange.

Makoto Nakamura

The Transformation of Commutative Phase Space to Noncommutative one and Lorentz-like Bopp's Shift forms

Noncommutative phase space of arbitrary dimension is discussed.
We introduce momentum-momentum noncommutativity in addition to
coordinate-coordinate noncommutativity. We find an exact form for the
linear coordinate transformation which relates a noncommutative phase
space to the corresponding ordinary one.
By using this form, we show that a noncommutative phase space of
arbitrary dimension can be represented by the direct sum of two
dimensional noncommutative ones.
In two dimension, we obtain the transformation which relates a
noncommutative phase space to commutative one. The transformation has
Lorentz transformation-like forms and can also describe the Bopp's shift.

Yu Song-Ju

Self-consistent sources for integrable systems in (2+1) dimensions by bi-differential calculus with SU(N)

Our research offers a unique perspective on the origin and structure of self-consistent source extensions of integrable equations, focusing specifically on the role of binary Darboux transformations. They arise via a deformation of the potential central to this method. For example, we obtain matrix versions of self-consistent source extensions of the KdV, KP, and discrete KP equation. By construction, these systems are accompanied by a hetero binary Darboux transformation, which generates solutions for such a system from a source-free system solution and solutions for an associated linear system and its adjoint. The essence of all this is encoded in universal equations in the framework of bi-differential calculus with SU(N).

Jonathan Stepp

Studying the attractive SU(N) Fermi-Hubbard model with determinant quantum monte carlo

Recent advances in microwave shielding of ultracold molecules have led to increased control of large numbers of polar molecules. In addition, new results show that shielded polar molecules exhibit an SU(N) symmetry about their low-lying hyperfine states. Motivated by the potential of using these molecules as a quantum simulator, we have studied the SU(N) Attractive Fermi-Hubbard model on a 2d square lattice. Using a Determinant Quantum Monte Carlo method with a non-standard Hubbard-Stratonovich transformation, we have demonstrated the existence of a finite-temperature charge-density wave phase and found evidence of a quantum phase transition in the Attractive SU(3) case. We also demonstrate that our method is easily extensible to higher N values and is sign-problem free for even values of N.

Kouichi Toda

Non-isospectral Lax pairs and related integrable equations in (2+1) dimensions

We will present explicit formulations of linear problems, so-called Lax equations, with non-isospectral parameters relevant to (2+1) dimensional versions of celebrated nonlinear integrable hierarchies. These have the SU(N) gauge potentials. Their exact solutions and conserved quantities may also be presented.

Yu Wang

Mott insulating states of the anisotropic SU(4) Dirac fermions

We employ the large-scale quantum Monte Carlo simulations to investigate the Mott-insulating states of the half-filled SU(4) Hubbard model on the square lattice with a staggered-flux pattern. The noninteracting band structure that evolves from a nested Fermi surface at zero flux to isotropic Dirac cones at 𝜋 flux, exhibits anisotropic Dirac cones as the flux varies in between. Our simulations show transitions between the three phases of the Dirac semimetal, antiferromagnet, and valence-bond solid. A direct continuous transition between the antiferromagnetic phase and the valence-bond-solid phase is realized via varying the flux in the Mott regime. The simulated critical exponents remarkably agree with those of SU(4) 𝐽−𝑄 model. Inside the valence-bond-solid phase induced by the flux, the plaquette valence-bond state with vanishing single-particle gap is identified. At strong coupling, the valence-bond-solid phase disappears and the Mott-insulating state is always accompanied by antiferromagnetic ordering, regardless of the magnitude of the flux.

Coexisting Néel and charge density wave orders in attractive three-color fermions

In optical lattices attractive ultracold fermions with three hyperfine-spin components (colors) can form three fermionic configurations depending on interactions: unbound fermion, on-site trion and off-site trion, leading to the coexistence of multiple Fermi species in the ordered phase, which manifests that the attractive three-color fermions are unique from other correlated fermion systems and may host intriguing phases and phase transitions. At temperature below the superexchange energy scale, we employ the determinant quantum Monte Carlo (QMC) method to investigate the phases and phase transitions in the half-filled attractive three-color Hubbard model on a honeycomb lattice where Hubbard interactions are color-dependent (anisotropic interactions) and the coupling
between color 3 and colors (1, 2) serves as a control parameter. In the coupling regime where on-site and offsite trions coexist, our QMC simulations demonstrate coexisting Néel and charge density wave orders which are common in condensed matter but rare in ultracold atoms. At weak coupling where the color superfluid (CSF) order is scattered by color-3 fermions, we find that very small coupling of color 3 with colors (1, 2) can destroy
the CSF order and the vanishing of the CSF order is not immediately accompanied by the emergence of the on-site trionic phase, which strikingly disagrees with the prevalent results of dynamical mean-field theory. The underlying mechanisms of the coexisting charge/spin orders and the CSF order breaking are also presented based on intuitive physical pictures.

Trion states and nonuniversal charge-density-wave transitions of attractive SU(3) ultracold fermions

Earlier works on attractive SU(3) ultracold fermions have mainly focused on the phase transition between the color superfluid state and the onsite trionic state. We have performed the projector quantum Monte Carlo (QMC) simulations of the half-filled attractive SU(3) Hubbard model on a honeycomb lattice, which shows that the off-site trion forms a local bound state and coexists with on-site trions in the charge density wave (CDW) phase. The critical exponents ν = 0.82(3) and η = 0.58(4) determined by the projector QMC simulation remarkably disagree with those of the N = 3 chiral Ising universality class suggested by the effective Gross-Neveu-Yukawa theory. We have also investigated the effects of trions on finite-temperature properties of the attractive SU(3) fermions by performing the determinant QMC simulations. Remarkably, the finite-temperature CDW transitions exhibit nonuniversal behavior in the half-filled attractive SU(3) Hubbard model, namely, the critical exponents vary with the Hubbard interaction.

Han Xu

Preparing Gutzwiller wave function for attractive SU(3) fermions on a quantum computer

We implement the Gutzwiller wave function for attractive SU(3) fermion systems on a quantum computer using a quantum-classical hybrid scheme based on the discrete Hubbard-Stratonovich transformation. In this scheme, we express the nonunitary Gutzwiller operator as a linear combination of unitaries involving two-qubit fermionic Givens rotation gates. The fermionic Givens rotations are employed to the register qubits encoding different fermion colors on each site. Two complementary approaches are reformulated to perform the sum over the auxiliary fields. The first approach probabilistically prepare the Gutzwiller wave function on the register qubits, but the measurement on ancilla qubits are necessary. Because of its probabilistic outcomes, the success rate is studied as a function of the variational parameter on different lattices when the Fermi-sea trial state and the BCS-like trial state are considered. The second approach utilizes the importance sampling technique to solve the Gutzwiller variational problem where the expectation values of observables are the central objectives. The proposed scheme is examined by calculating the energies and triple occupancy of the attractive SU(3) Hubbard model within the context of the digital quantum simulation. Moreover, experiments on a trapped-ion based quantum computer are carried out for the two-site attractive SU(3) Hubbard model, where the raw data are in good agreement with the exact results within the statistical errors.

Shintaro Yamamoto

Spectral flow of fermions in the CP2 (anti-)instanton, and the sphaleron with vanishing topological charge

The spectral flow is ubiquitous in the physics of soliton-fermion interacting systems. Due to the effect of the topology of such systems, fermion zero modes (or spectral flows) arise and the fermion densities are localized. We study the spectral flows related to a continuous deformation of background soliton solutions, which enable us to develop new insights into the emergence of fermionic zero modes and the localization mechanism of fermion densities. In this talk, we first introduce a class known as the texture type of topological solitons and see that the concept of spectral flow naturally appears through the deformation degree of freedom of the solitons. As an illustrative example, we investigate a $\mathbb{C}\mathrm{P}^2$ nonlinear sigma model in which there are the (anti-) instantons and also the sphalerons with vanishing topological charge. The standard Yukawa coupling of the fermion successfully generates infinite towers of the spectra and the spectral flow is observed as increasing size of such solitons. Within a certain range of the size, the localization of the fermions on the solitons appears. The avoided crossings occur at multiple points in the exchange of the flows, indicating a manifestation of the fermion exchange of the localizing aspect.

Zewen Zhang

Unit-filling SU(3) Fermi-Hubbard Model with flavor imbalance

Motivated by ongoing experiments with alkaline-earth atoms in optical lattices, we investigate the phases of the square lattice SU (3) Fermi-Hubbard model with spin flavor imbalance using Hartree-Fock theory, focusing on the case with one-atom per site average density. Previous calculations on the flavor-balanced system predict the existence of a Mott transition and ordered phases in the Heisenberg limit. Our results suggest that at intermediate interaction strengths, multiple new magnetic and density orders appear. We also show that these magnetic ordered phases are robust at small spin flavor imbalance, and that new phases appear upon large flavor imbalance. The mean-field results provide distinctive signatures to search for with ongoing experiments using quantum gas microscopes.